中学受験専門 国語 プロ家庭教師 細川
■難関中学 受験対策
■国語読解・記述指導
■東京23区・千葉県北西部
■中学受験を専門に、国語のプロ家庭教師として活動しています。
■家庭教師とご家庭との直接契約(個人契約)によるご指導です。
■お問い合わせ
■047-451-9336
■午前10時~午後2時
■まずはお電話でお問い合わせください。
■体験授業の日程が決定してのち、こちらの『メールフォーム』よりメールをお送りください。追って当方よりご案内メールをお送りいたします。
★子どもたちとの新たな出会いを楽しみにしています!
■論理パズル
■『受験国語 選択肢の判別 111の視点(無料)』
■最新版がダウンロードされたかご確認ください。
■記事
・B5正味68ページ(B4両面18枚/表紙1枚含む)
・本編約110,000字
■PDFデータ量
・7.79MB
■プリンター設定
・B4用紙
・印刷の向き(横)
・両面印刷
・短辺とじ
※両面で上下反対に印刷されないよう、数ページ分でテスト印刷をしてください。
■製本
・両面印刷後、用紙をしっかりと二つ折りにし、ページ順に揃えて重ね、『回転式ホチキス』で「中(なか)とじ」します。
・ホチキスは、背(外側)からノド(内側)に向けて打ちます。また、天地からそれぞれ6~7cmの位置に一か所ずつ打つと冊子が安定します。
■補足
・本資料は一見難しい内容に思えるかもしれませんが、大人の助力により(事前に読み込みが必要)、手順を踏んで説明すれば、小学5、6年生にもしっかりと理解させることが可能です。
・本資料は国語の読解問題における選択肢を思考力や論理力、分析力や検討力等によって正しく判別するための育成教材であるため、コツ、裏技といった安直な解決法は記載していません。(※ただし、一部ネタも含みます)
・内容的に中学生や高校生の学習にも利用できます。
■頒布自由
・本資料(PDFデータ、または冊子)を必要とする各人、各所への頒布は自由です。
各種論理

■三段論法(演繹法)・帰納法・背理法・論理的飛躍・弁証法・類推・仮説形成・詭弁論理など、各種論理の解説。
■『選択肢の判別 111の視点(PDF/無料)』:本ページにて記載した『論理パズル』、『数理パズル』、および『各種論理』についても掲載していますのでご利用ください。
目 次
■論理パズル・数理パズル
①『消えた1,000円の謎』(心理操作と前提操作)
②『勝利をつかめ!』(前提を疑う)
③『天使と悪魔と人間』(背理法と消去法)
④『犯人を見つけろ! ~てへぺろ行方不明事件』(背理法と消去法)
⑤『魂を返せ!』(背理法と消去法)
⑥『Aさんの帽子は何色か?』(背理法と消去法)
⑦『今週のジャイアン当番』(背理法と消去法)
⑧『5人の宇宙人』(背理法と消去法)
⑨『偽金貨はどれだ?』(思考の転換・組み合わせ)
⑩『ライオンと羊とキャベツを運ぼう!』(思考の転換・組み合わせ)
⑪『二つの砂時計』(思考の転換・組み合わせ)
■参考
①三段論法
②前提操作(前提のすり替え・条件トラップ)
③矛盾
④背理法
④仮説形成(アブダクション/リトロダクション)
⑤アンカリング効果
※三段論法(演繹法)、帰納法、論理的飛躍、背理法、弁証法、類推(類比)、仮説形成(アブダクション/リトロダクション)等の詳細については『各種論理』のページをご参照ください。
① 消えた1,000円の謎

■問題
・三人の客がレストランで食事をし、一人10,000円ずつ、合計30,000円を支払いました。客の一人が、「少しまけてよ」と持ちかけると、レジ係は店主から「5,000円を返金してよい」と言われました。するとレジ係は、5,000円だと3人で割り切れないと考え、こっそりと2,000円を自分のポケットに入れ、客には3,000円だけを返金しました。
・さて、客は一人9,000円ずつ支払ったことになるので、支払いの合計金額は27,000円です。これにレジ係がくすねた2,000円を足すと、合計29,000円になります。客が最初に支払ったのは30,000円だったはずです。1,000円はどこへ消えてしまったのでしょう。
■答え
・ドナルド君:店主が5,000円の値引きを認めたのだから、本来客側は25,000円を支払えば済んだはずだ。にもかかわらず、客が支払った金額は27,000円となった。では、この2,000円分の金額は一体どこから現れたのか。
・近平君:レジ係が2,000円をくすねさえしなければ、客は25,000円を支払うだけでよかったのだから、その「2,000円分はレジ係のくすねた金額」に当たるんだよね。
・ドナルド君:「27,000円の中にレジ係のくすねた2,000円分が含まれている」というのなら、問題文の
「27,000円に2,000円を足す」という計算は、「レジ係のくすねた2,000円」を2回足すということになるだろう。
・近平君:なるほど! 問題文自体にウソが仕込まれているんだ! 「総額30,000円のお金の動き」として見るのなら、客側に返金された3,000円が計算に含まれていないのも、そもそもおかしい。
・ドナルド君:本当の計算としては、「店の売り上げとなる25,000円」に「レジ係の手に渡る2,000円」を加え、さらにそれに「客に返金された3,000円」を加えると、問題文にある「客が最初に支払った30,000円」と一致する。
・近平君:よし、問題文を正してみるよ! 「客は一人9,000円ずつ支払ったことになるので、支払いの合計金額は27,000円です。ただし、この金額には、レジ係がくすねた2,000円分、つまり、本来はレジ係が客に返金すべき2,000円分が含まれていますが、客側はそれを全く知りません。この『店側に動いた(客が支払った)27,000円』に『客側に動いた(実際に返金された)3,000円』を加えると、合計金額は30,000円となり、客が店に最初に支払った金額と一致します。」
・近平君:ところで、問題文に虚偽の計算が仕込まれていたことは確認できたけれど、どうしてそれに気づくことができなかったのだろう。不思議だなあ……。
・ドナルド君:問題文に含まれている、「(客による)支払いの合計金額は27,000円」、「客が最初に支払った30,000円」という表現は、つい「客側の視点」で一方向的に文脈を捉(とら)えてしまう。それで、問題の読み手はそこに意識が強く引っ張られて、逆に「店側の視点」から見たお金の流れが把握しづらくなるんだ。※アンカリング効果
・近平君:確かに、さっきの説明のように、「客側が支払った27,000円は、店側が受け取った27,000円」だと視点を切り替えて捉え直せば、店側から見たお金の流れが確認できて理解が簡単だものね。計算上の誤りがすぐにわかった。
・ドナルド君:ところが、「視点が固定されて切り替えができずにいる」と、「客側が支払った27,000円にはレジ係のくすねた2,000円分が含まれている」という「前提条件」が掴みづらくなり、読み手の思考からそれがすっぽりと抜け落ちてしまう。だから、読み手は「レジ係のくすねた2,000円」が二重に加算されていることに気づけず、筋道(すじみち)を見失って宙に浮いたようになってしまうんだ。 ※前提操作(『前提の消失/前提の隠匿(いんとく)』)
・近平君:はじめは訳(わけ)がわからなくて狐につままれたようだったよ。「問題文自体に虚偽が仕込んである」だけでなく、「心理的な誘導トリック」も使われていたのか。作為的に表現を操作して読み手の視点を固定し、その後の判断に歪(ゆが)みを生じさせる「暗示トリック」にかかってしまった、というわけだね。※アンカリング効果
・ドナルド君:おまけに、思考に筋道を立てるうえでの重要な情報である「前提」の一つを見失わせて混乱させる「論理トリック」も仕組まれている。 ※前提操作(『前提の消失/前提の隠匿(いんとく)』)
・近平君:「レジ係の盗みを客側が全く知らない」という状況も、「レジ係がくすねた2,000円を足す」という虚偽の計算を読み手に信じ込ませるための暗示材料となっているね。
・ドナルド君:しかもだ、「これにレジ係がくすねた2,000円を足すと」のように「偽(にせ)の計算を当然の条件として直ちに与えられる」と、読み手は自然とこの誘導に乗せられて、この条件を前提の一つとして新たに筋道を立て直そうと試みる。だが、そもそも「偽の前提」を基(もと)にして計算が合うはずがない。これもまた、論理的誘導の一手法というわけだ。 ※前提操作(『条件トラップ』)
・近平君:妖(あや)し気(げ)に立ち現れては、ふいと消えてしまう「物の怪(け)」の変幻(へんげん)のように、「前提の変幻」に翻弄(ほんろう)されて、考えれば考えるほど、いっそう混迷(の淵(ふち)に深く陥(おちい)ってしまうというわけか。それにしても、ものごとを理解するには「視点の切り替え」や「相対的視点からの検討」が大事なんだね。それと、「国語力」と、「論理的思考力」もだ!
※物(もの)の怪(け):人にとりついて祟(たた)りをする妖怪(ようかい)・死霊(しりょう)・生霊(いきりょう)の類(るい)。
※変幻(へんげん):出没や変化をすばやくすること。
※翻弄(ほんろう):思いのままにもてあそぶこと。
※参照
・『アンカリング効果(初期値提示誘導)』
・『三段論法』
・『前提操作(前提のすり替え・条件トラップ)』
② 勝利をつかめ!
■問題
・「赤・青・黄・緑」の箱のどれかに、『勝利』が入っています。勝利は、一つの箱にだけ入っているのか、複数の箱に入っているのかは分かりません。勝利を手に入れたいあなたは、どれか一つの箱だけをもらえることになりました。
ただし、……
①赤の箱に勝利があるときには、青の箱にも入っている。
②緑の箱に勝利が無いときには、黄色の箱にも入っていない。
③緑の箱に勝利が無いときには、青の箱にも入っていない。
・情報②と③の、『緑の箱に勝利が無いときには』から始めて考えを進めてゆくと、『ある矛盾』に突き当たります。そして、「その矛盾が生じた、そもそもの理由」に気づくと、答えがわかります。どの色の箱に勝利が入っているのか考えてみましょう。
■答え
(1)情報②と③により、「緑の箱に勝利が無いときには」、「黄色の箱にも、青の箱にも入っていない」。
(2)「緑の箱」にも、「黄色の箱」にも、「青の箱」にも入っていないのであれば、勝利は「赤の箱に入っている」ことになる。
(3)しかし、「赤の箱に入っている」のであれば、情報①により「青の箱にも入っている」ことになって、(1)の内容と矛盾する。
(4)一般法則として、前提が誤っていると、論理は誤って展開し、誤った結論が導かれる。 ※仮説形成(アブダクション/リトロダクション)
(5)そうであるなら、(3)の矛盾は、「緑の箱に勝利が入っていない」とする当初の『前提』がそもそも誤りであったために生じたのだと考えられる。
(6)つまり、『誤った前提』をもとに考えを進めたために、この矛盾に突き当たったということだ。
(7)よって、当初の「前提を逆転」し、勝利が「緑の箱に入っている」と捉(とら)え直すことで、この矛盾が解消される。
※参照
・『背理法』
・『仮説形成(アブダクション/リトロダクション)』
■口頭でのアウトプット(説得的論証/再構築化)に挑戦!
・上の解説内容をもとにして、今度は大人を聞き手として、あなた自身がこの問題の解き方を口頭で説明してみてください。ただし、あなたの考え方が聞き手に正確に理解されるよう、説明する内容を予(あらかじ)めよく整理したうえで、一つひとつ段階を踏(ふ)みながら論理的に、また、伝わりやすさを工夫して説明に臨(のぞ)みなさい。
③ 天使と悪魔と人間
■問題
・天使は常に本当のことを言い、悪魔は常にウソをつき、人間は本当のことを言うこともあれば、ウソをつくこともあります。A、B、Cの3人が、次のように言いました。
A:私はね、天使ではありませんよ。
B:私はね、人間ではありませんよ。
C:私はね、悪魔ではありませんよ。
・『もしAが天使なら』、『もしAが悪魔なら』のように仮定して『矛盾はないか』確かめていくと、A、B、C3人の正体が明らかになります。では、問題の解明に挑(いど)んでみましょう!
■答え
①もしAが天使なら、天使がウソを言っていることになるので矛盾する。だから、Aは天使ではない。
②また、もしAが悪魔なら、悪魔が本当のことを言っていることになるので矛盾する。だから、Aは悪魔ではない。
③以上により、「Aは人間」であると考えられる。
④次に、もしBが天使なら、本当のことを言っていることになるので矛盾しない。だから、「Bは天使」である。
⑤また、もしBが悪魔なら、悪魔が本当のことを言っていることになるので矛盾する。だから、Bは悪魔ではない。
⑥以上により、「Aが人間」、「Bが天使」、「Cが悪魔」であるとわかる。3人それぞれの発言として、そこに矛盾はない。
※参照
・『背理法』
■口頭でのアウトプット(説得的論証/再構築化)に挑戦!
・上の解説内容をもとにして、今度は大人を聞き手として、あなた自身がこの問題の解き方を口頭で説明してみてください。ただし、あなたの考え方が聞き手に正確に理解されるよう、説明する内容を予(あらかじ)めよく整理したうえで、一つひとつ段階を踏(ふ)みながら論理的に、また、伝わりやすさを工夫して説明に臨(のぞ)みなさい。
④ 犯人を見つけろ! ~カオスにおける調和とは~
■問題
・あるクラスで、『てへぺろ』行方(ゆくえ)不明事件」が発生しました。一人の犯人だけがウソをつき、残りの二人は本当のことを言っています。それでは、三人の容疑者の供述を聞いてみましょう。
A君:B君が絶対に犯人だよ。僕(ぼく)は『てへぺろ』を隠(かく)していない。
B君:C君が犯人だ。僕も『てへぺろ』を隠していない。
C君:僕は犯人じゃない。『てへぺろ』なんか隠してないよ。
・この三人の中に、『てへぺろ』をどこかへ隠した者が一人だけいます。『もしA君が本当のことを言っているとしたら』から始めて『そこに矛盾はないか』を確かめていくと、誰が犯人であるかがわかります。では、事件の解決に挑(いど)んでください!
■答え
・茂君:「絶対に」と言っているのが事実であるならば、これは絶対にA君を怪(あや)しまねばならない。
・佳彦君:印象で決めつけるものじゃないよ!!!
・恋宝さん:印象だけじゃダメなんですか?!
・堀ゑ門:何言ってんの?! ダッセ! お前、終わってんだよ!!
・正広君:ケケケ! 太一、おめぇもかよ!
・洋文君:まず、もしA君が本当のことを言っていると仮定すると、「C君が犯人だ」と言うB君はウソを言っていることになる。一人だけがウソを言っているのだから、残ったC君は本当のことを言っていると考えていい。この理屈だと、特に矛盾は起きないね。
・綾香さん:今度は、もしB君が本当のことを言っていると仮定すると、「自分は犯人ではない」と言うC君の言葉がウソになる。C君が怪しいわ。
・雄一郎君:ちょっと待った! でも、もしB君が本当のことを言っていると仮定すると、犯人ではないはずの「B君が犯人だ」と言うA君もウソを言っていることになるよ。一人だけがウソを言っているはずなのに、二人がウソをついているとなると、矛盾だよ。
・鉄夫君:やはりB君が怪しいな!
・尚樹君:疑惑は……
・清美さん:疑惑はさらに深まった! てへぺろっ!!!
・智子さん:ダン!!! (机を激しく叩(たた)く音) あんたは一生お黙(だま)りなさい! ベゴッ!!! (投げつけた靴(くつ)が清美さんの顔を直撃した音) 一応C君も調べてみようよ。もしC君が本当のことを言っていると仮定すると、「C君が犯人だ」というB君はウソを言っている。
一人だけがウソを言っているのだから、A君は本当のことを言っているのね。この理屈で考えても、やっぱり矛盾は起きないわ。
……て、てへぺろ (意識を取り戻した清美さんの声)
・創平君:世界を操(あやつ)っている闇(やみ)の勢力の仕業(しわざ)だよ!
・宗男君:よし、B君を逮捕(たいほ)しろ!
・竜兵君:聞いてないよ!!!
・憲寿(のりとし)君:『どこが違うのか』、その『定義』を聞いているんです!!!
・伸二君:……は? 『定義』の話ではなく、『相違点』の話でいいですよね?
・孝志君:ぶっこわーすを、ぶっこわーす!
・ひろゆき君:それっていうのも、アリかなって思うんスよね。
・太郎君:だったら変えよう、オイラと一緒に!
・瑞穂(みずほ)さん: どっこい! どっこい! がんこに平和! 級長守れ!! クラスが一番!!!
・人志君:ん~、なんか、五・七・五みたいなん?
・進次郎君:30年後の自分は何歳かなと、ずっと私は考えていました。
・たけし君:ちょっと何言ってるかわからない。
※参照
・『背理法』
■口頭でのアウトプット(説得的論証/再構築化)に挑戦!
・上の解説内容をもとにして、今度は大人を聞き手として、あなた自身がこの問題の解き方を口頭で説明してみてください。ただし、あなたの考え方が聞き手に正確に理解されるよう、説明する内容を予(あらかじ)めよく整理したうえで、一つひとつ段階を踏(ふ)みながら論理的に、また、伝わりやすさを工夫して説明に臨(のぞ)みなさい。
⑤ 魂(たましい)を返せ!
■問題
・あるとき、ラップにくるんで冷蔵庫に大切に保存しておいた『魂』が、誰かに食べられてしまった。そこで、Aは次のように言い、BとCもまた、何かを言った。
A:「犯人はBだよ」
B:「……だ」
C:「……だよん」
・後(のち)に得られた情報は、以下の三つだった。
①犯人は、A、B、Cのうち、1人である。
②本当のことを言ったのは、犯人だけである。
③ウソをついているのは、無実の人である。
・『もしAが本当のことを言っているのなら』、『もしAがウソをついているのなら』のように仮定して『矛盾がないか』を確かめていくと、真犯人をつきとめることができます。
■答え
(1)「もしAが本当のことを言っているのなら」、条件②により、「本当のことを言ったAが犯人」だ。
(2)そして、そのA本人による発言内容もまた本当なのだから、「Bも犯人」である。
(3)しかし、AとBが二人とも犯人であるというのは、「犯人は1人しかいない」という条件①と矛盾する。
(4)よって、Aは本当のことを言っておらず、条件③により、「ウソをついたA本人は無実」であると考えられる。
(5)逆に、「もしAがウソをついているのなら」、条件③により、「Aは無実」だ。これは(4)の結論とも一致する。
(6)そして、A本人による発言内容もまたウソなのだから、「Bは無実」である。
(7)よって、「AもBも無実」であるなら、残された一人、「Cが犯人」であるとわかる。条件①、②、③の全てを満たす以上の考え方に矛盾はない。
※参照
・『背理法』
■口頭でのアウトプット(説得的論証/再構築化)に挑戦!
・上の解説内容をもとにして、今度は大人を聞き手として、あなた自身がこの問題の解き方を口頭で説明してみてください。ただし、あなたの考え方が聞き手に正確に理解されるよう、説明する内容を予(あらかじ)めよく整理したうえで、一つひとつ段階を踏(ふ)みながら論理的に、また、伝わりやすさを工夫して説明に臨(のぞ)みなさい。
⑥ Aさんの帽子は何色か?
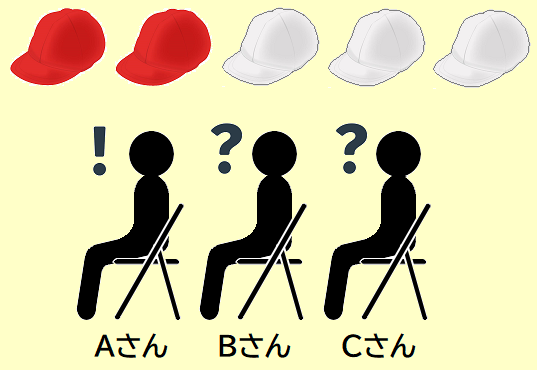
■問題
・赤い帽子(ぼうし)が二つ、白い帽子が三つあります。Aさん、Bさん、Cさんの三人の生徒が縦に順に並び、前を向いたまま椅子(いす)に腰(こし)かけました。その後、それぞれが5つの帽子の中のどれかを被(かぶ)りました。3人とも、自分が被っている帽子の色はわかりませんが、3番目にいるCさんには、前の二人が被っている帽子の色が見えており、2番目にいるBさんには、最前列にいるAさんの帽子の色が見えています。
・先生が、まずCさんに自分の帽子の色をたずねると、「わかりません」と答えました。次に、Bさんに同じ質問をすると、やはり「わかりません」と答えました。Aさんに同じ質問をすると、「わかりました」と答えました。
・そこで、『もしAさんとBさんが二人とも赤い帽子を被っていたのなら』から始めて、最前列にいるAさんは自分が何色の帽子を被っているとわかったのかを考えてみましょう。
■答え
①もしAさんとBさんが二人とも赤い帽子を被っていたのなら、Cさんは「自分の帽子は白です」と答えられたはずです。もともと赤い帽子は二つしかないからです。
②でも、Cさんは「わかりません」と答えたので、この仮定は正しくないことになります。だとすると、「AさんとBさんは、二人とも白い帽子を被っていた」か、「AさんとBさんのそれぞれが、赤か白、いずれかの帽子を被っていた」のだと考えられます。
③次に、もしAさんが赤い帽子を被っていたのなら、Bさんは「自分の帽子は白だ」とわかったはずです。なぜなら、最初のCさんの言葉から「AさんとBさんが二人とも赤い帽子を被っている」ことが既(すで)に否定(ひてい)されているからです。
④ところが、Bさんは「わかりません」と答えました。
⑤そこで、Aさんは、「自分の帽子が赤でないのなら、白だ」とわかったのです。
※参照
・『背理法』
■口頭でのアウトプット(説得的論証/再構築化)に挑戦!
・上の解説内容をもとにして、今度は大人を聞き手として、あなた自身がこの問題の解き方を口頭で説明してみてください。ただし、あなたの考え方が聞き手に正確に理解されるよう、説明する内容を予(あらかじ)めよく整理したうえで、一つひとつ段階を踏(ふ)みながら論理的に、また、伝わりやすさを工夫して説明に臨(のぞ)みなさい。
⑦ 今週のジャイアン当番
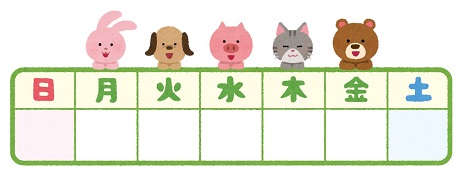
■問題
・今週のジャイアン当番は、ルイ君、サラさん、メル君、ルルさん、レオ君の5人です。以下の情報をもとに、月曜日から金曜日まで、誰がジャイアン当番なのかを特定してください。
①ルイ君はレオ君の数日前が当番です。
②サラさんの当番はルルさんより後です。
③メル君の当番はルルさんの2日前です。
④レオ君は木曜日が当番です。
■答え
(1)④の情報により、レオ君の当番は木曜日で確定している。
(2)①によれば、ルイ君の当番はレオ君の「数日前」なので、「一日前」の水曜日ではなく、月曜日か火曜日のいずれかである。
(3)もしメル君が水曜日だとしたら、③によりルルさんが2日後の金曜日となるが、それだとサラさんが土曜日以降となってしまい、「当番は金曜日まで」という条件に合わず、矛盾(むじゅん)する。だから、メル君は水曜日ではない。
(4)もしメル君が火曜日だとしたら、③によりルルさんが2日後の木曜日となってしまい、木曜日で確定しているレオ君と曜日が重なり、矛盾する。だから、メル君は火曜日ではない。
(5)もしメル君が月曜日だとしたら、③によりルルさんは2日後の水曜日となり、また、②によりサラさんが金曜日であっても矛盾しない。
(6)さらに、もしメル君が月曜日だとしたら、火曜日がルイ君であっても①と矛盾しない。
(7)以上により、月曜日はメル君、火曜日がルイ君、水曜日がルルさん、木曜日がレオ君、金曜日がサラさんであると結論される。
※参照
・『背理法』
■口頭でのアウトプット(説得的論証/再構築化)に挑戦!
・上の解説内容をもとにして、今度は大人を聞き手として、あなた自身がこの問題の解き方を口頭で説明してみてください。ただし、あなたの考え方が聞き手に正確に理解されるよう、説明する内容を予(あらかじ)めよく整理したうえで、一つひとつ段階を踏(ふ)みながら論理的に、また、伝わりやすさを工夫して説明に臨(のぞ)みなさい。
⑧ 5人の宇宙人

■問題
・パッブー(A)、ピコペポ(B)、プルッパ(C)、ヨーギェル(D)、テレロ(E)という名の5人の宇宙人が地球にやって来て、それぞれが何かをしています。『地球儀がAかEであるのなら』から始めて考えを進め、どの宇宙人が何をしているのかを特定してください。
※考えを進めてゆきやすいよう、宇宙人の名称をアルファベット記号のみで、また、行動もキーワードのみで簡略化して構いません。
※ヒント:③を踏(ふ)まえ、次に①、その次に②を検討してみるといいよ。
①Dは地球儀(ぎ)を眺(なが)めているか、温泉につかっている。
②A、B、Cの3人は星を眺めてはいない。
③AかEのどちらかが、地球儀を眺めている。
④B、C、Dのうち1人が、宇宙船の修理をしている。
⑤居眠(いねむ)りをしているのは、Cではない。
■答え
(1)情報③により、地球儀がAかEであるのなら、①のDは地球儀ではない。だから、「Dは温泉」である。
(2)「Dが温泉」であるのなら、情報②の「星を眺めているのがDかE」なのだから、「Eが星」である。
(3)「Eが星」であるのなら、情報③の「Aは地球儀」である。ここまでで「Aが地球儀」、「Dが温泉」、「Eが星」と確定する。
(4)情報⑤により、Cは居眠りをしておらず、また、確定した「A、D、E」も居眠りをしていないのだから、この「A、C、D、E」以外の「Bが居眠り」となる。
(5)以上により、最後に残った「Cは宇宙船」である。
※参照
・『背理法』
■口頭でのアウトプット(説得的論証/再構築化)に挑戦!
・上の解説内容をもとにして、今度は大人を聞き手として、あなた自身がこの問題の解き方を口頭で説明してみてください。ただし、あなたの考え方が聞き手に正確に理解されるよう、説明する内容を予(あらかじ)めよく整理したうえで、一つひとつ段階を踏(ふ)みながら論理的に、また、伝わりやすさを工夫して説明に臨(のぞ)みなさい。
⑨ 偽(にせ)金貨はどれだ?

■問題
・金貨が沢山(たくさん)入った袋が三つあります。そのうちの一袋は全て偽(にせ)金貨です。本物の金貨は1枚100gですが、偽金貨は1枚当たり本物より10g重くなっています。偽金貨の袋がどれかを探したいのですが、秤(はかり)は一度だけしか使えません。偽金貨の袋を探すには、どうすればよいでしょう。
■答え
・一つ目の袋から1枚、次に二つ目の袋から2枚、続けて三つ目の袋から3枚金貨を取り出し、計6枚の金貨を秤に載(の)せればよい。
①もし三つの袋が全部本物の金貨であれば、取り出した金貨6枚分の重さを足すと、600gちょうどになる。
②もし一つ目の袋に入っているのが偽金貨なら、取り出した偽金貨1枚分だけ、つまり、10g重くなるから、秤では610gになる。
③もし二つ目の袋に入っているのが偽金貨なら、取り出した偽金貨2枚分、つまり、20g重くなるから、秤では620gになる。
④もし三つ目の袋に入っているのが偽金貨なら、取り出した偽金貨3枚分、つまり、30g重くなるから、秤では630gになる。
※テレビドラマ『刑事コロンボ』~「殺しの序曲」より
■口頭でのアウトプット(説得的論証/再構築化)に挑戦!
・上の解説内容をもとにして、今度は大人を聞き手として、あなた自身がこの問題の解き方を口頭で説明してみてください。ただし、あなたの考え方が聞き手に正確に理解されるよう、説明する内容を予(あらかじ)めよく整理したうえで、一つひとつ段階を踏(ふ)みながら論理的に、また、伝わりやすさを工夫して説明に臨(のぞ)みなさい。
⑩ ライオンと羊とキャベツを運ぼう!
■問題
・動物園の飼育員が、ライオン、羊、キャベツをボートで川の対岸に運ぼうとしています。
でも、……
(1)飼育員がそばにいないと、ライオンは羊を食べてしまう。
(2)飼育員がそばにいないと、羊はキャベツを食べてしまう。
(3)ボートには、飼育員の他にライオンか羊かキャベツのいずれか一頭(一つ) しかのせられない。
・『まず、羊をボートにのせ』から始め、ライオン、羊、キャベツを無事にすべて対岸に運ぶ方法を考えてください。
■答え
①まず、羊をボートにのせ、対岸に運ぶ。
②次に、飼育員が一人で戻り、ライオンをボートにのせて対岸に運ぶ。
③その後、羊をボートにのせて戻り、陸におろしてから、今度はキャベツを対岸に運ぶ。
④最後に飼育員がまた一人で戻り、羊をのせて対岸に運ぶ。
■口頭でのアウトプット(説得的論証/再構築化)に挑戦!
・上の解説内容をもとにして、今度は大人を聞き手として、あなた自身がこの問題の解き方を口頭で説明してみてください。ただし、あなたの考え方が聞き手に正確に理解されるよう、説明する内容を予(あらかじ)めよく整理したうえで、一つひとつ段階を踏(ふ)みながら論理的に、また、伝わりやすさを工夫して説明に臨(のぞ)みなさい。
⑪ 二つの砂時計

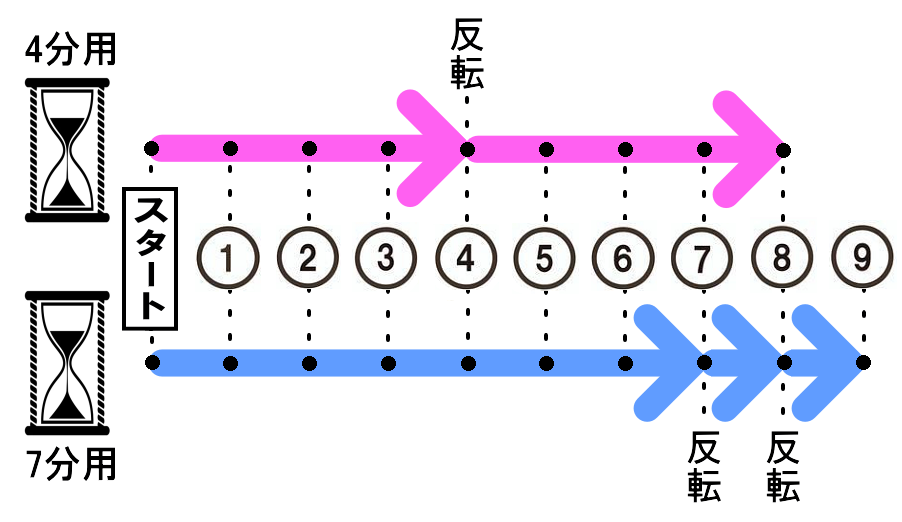
■問題
・ここに二つの砂時計があります。一つは「4分用」で、もう一つは「7分用」です。この二つの砂時計を用いて「9分」を計りたいのですが、どうすればよいでしょう。
■答え
①まず、二つの砂時計を同時にスタートさせます。
②「4分の砂時計」が終わったら、それを反転させます。この時点でスタートから4分経過しています。
③その3分後、「7分の砂時計」が終わったら、それを反転させます。この時点でスタートから7分経過しています。
④さらにその1分後、つまりスタートから8分経過時に「4分の砂時計」が終わります。そしてこの時、1分前に反転させたばかりの「7分の砂時計」を再び反転させます。「7分の砂時計」は、反転させたその時点で砂が「1分」の分量だけ残っているのですから、この砂が全て落ちた瞬間が、スタートからちょうど9分後となります。
■口頭でのアウトプット(説得的論証/再構築化)に挑戦!
・上の解説内容をもとにして、今度は大人を聞き手として、あなた自身がこの問題の解き方を口頭で説明してみてください。ただし、あなたの考え方が聞き手に正確に理解されるよう、説明する内容を予(あらかじ)めよく整理したうえで、一つひとつ段階を踏(ふ)みながら論理的に、また、伝わりやすさを工夫して説明に臨(のぞ)みなさい。
■参考
① 三段論法(演繹法)
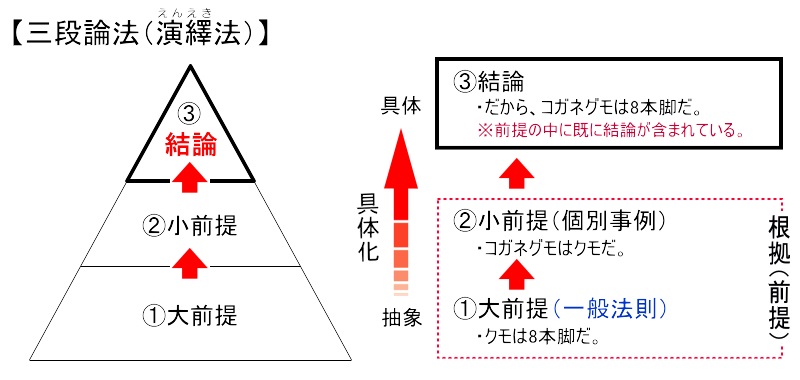
■三段論法とは、「二つの前提」から「一つの結論」を導き出す推論形式で、論理展開の基本とされます。「前提」とは、「結論」を導くための「根拠となる条件」のことです。「前提」は、「論理の土台」であり、正しい論理や因果関係を組み立てるうえでの重要な要素となります。
①【大前提】で「一般法則(全体のことがら)」を述べます。
例:クモは8本脚だ。
②【小前提】で「個別事例(一部のことがら)」を述べます。
例:コガネグモはクモだ。
③【結論】二つの前提を「根拠」として、「結論」を導きます。
例:だから、コガネグモは8本脚だ。
※前提に既に結論が含まれているために完全に納得される。
② 前提操作
■前提のすり替え
・ある主張(結論)が成り立つための大もととなる「本来の前提」を、「それとは合致(がっち)しない別の前提」にすり替えたうえで論理展開すること。
・花子さん:夏休みの宿題、もう全部終わったもんね! (正しい前提:自力で宿題を処理)
・愛子さん:先生にバレなきゃいいね! (別の前提:花子がズルい手を使って宿題を処理)
・花子さん:もうっ! 違うってば! 意地悪!
・「花子さんは実際に自分一人の力で全ての宿題を早く片付ることができた(正しい前提)」のですが、愛子さんはその「事実=前提」を承知しながら、「花子さんが何かズルい手を使って宿題を早く片付けることができた」という「別の前提」に「わざと変更=すり替え」を行って意地悪く応答しました。
■条件トラップ
・【[A]これにレジ係がくすねた2,000円を足すと(条件)+[B]合計29,000円になります】のように、【Aを条件(前提)として+B(となる/である)】の形式で説明されるが、そもそも[A]という条件(前提)が虚偽(きょぎ)、もしくは不正確である。
誘導に都合の良い《虚偽の条件[A]》を「前提」として、しれっと[B]が続くため、よく注意して文脈把握(はあく)しないと《条件[A]》の虚偽による誘導に気づくことが難しい。「前提のすり替え」の一種。
③ 矛盾

■矛盾とは、二つの主張のつじつまが合わないこと。論理的な食い違(ちが)いがあり、筋(すじ)が通らないこと。撞着(どうちゃく)ともいう。
・昔、中国の楚(そ)の国で、矛(ほこ)と盾(たて)を売っていた商人が、「この矛は、どんなにかたい盾をも突(つ)き通すことができる。また、この盾は、どんなに鋭利(えいり)な矛であっても突き通すことができない」と言って誇(ほこ)った。
すると、見物人が、「では、その矛でその盾を突いたらどうなるか」と問(と)うたところ、商人は返答に窮(きゅう)してしまった。
・「この矛はどんなにかたい盾をも突き通すことができる」という主張[A]と、「この盾はどんなに鋭利な矛であっても突き通すことができない」という主張[B]は、論理的に整合しない。つまり、[A]の主張を「正しい」と認めた場合は[B]の主張が「誤(あやま)り」となり、逆に[B]の主張を「正しい」と認めた場合は[A]の主張が「誤り」となって、二つの主張を両立させることが不可能なのだ。
④ 背理法
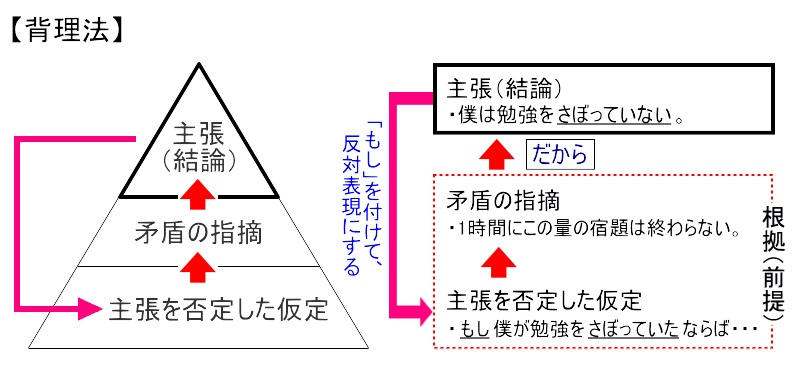
■「背理(はいり)法」とは、「①:ある主張」について、「②:『もし』を付けて反対表現にし(主張を否定した仮定をし)」、それにより生じる「③:矛盾」を示すことで「仮定の誤り」を導き、結果的に「④:当初の主張が正しい」ことを証明する方法です。ただし、主張(結論)が本当に正しいかどうかは検証によって確かめられる必要があります。
①「お母さん、僕、勉強サボってないよ」【主張】
②「「もし勉強をサボっていたのなら……」【主張を否定した仮定】
③「一時間にこれだけの宿題が終わるはずがないよ」【矛盾の指摘】
④「だから、僕は勉強をサボってない!」【結論=主張】
・別の例文
①【主張】「私は犯人ではない」
②【主張を否定した仮定】「もし私が犯人なら」
③【矛盾の指摘】「犯行時刻に、犯行現場であるA町にいたはずだ。でも、その時私はB町にいたし、証人もいる」
④【結論=主張】「だから、私は犯人ではない」
⑤ 仮説形成(アブダクション/リトロダクション)
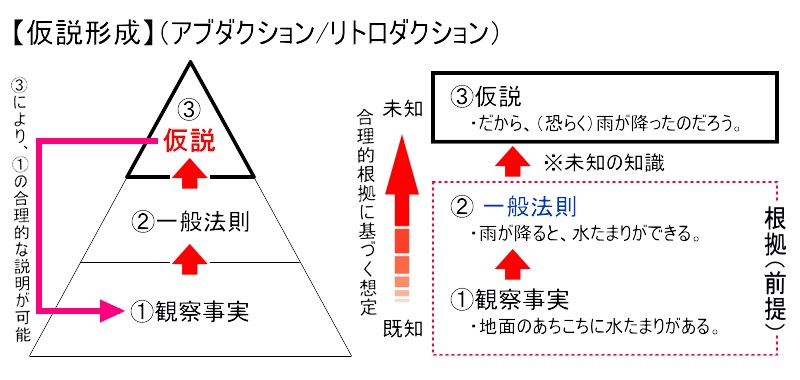
■ある「観察事実」をもとに、その原因を探るため、「一般的法則や知識・情報等」を照らし合わせ、それを「前提」として「合理的な説明を想定」する推論法を「仮説形成」(アブダクション/リトロダクション)といいます。
■仮説形成の例①
・前提①:地面のあちこちに水たまりがある。【観察事実】
・前提②:雨が降ると、水たまりができる。【一般法則】
・結論:だから、(恐らく)雨が降ったのだろう。【仮説】
・「仮説形成」は、「既知(きち)の知識」をもとにして「未知の知識」を新たに得るための強力な思考法の一つです。ただし、想定した仮説が必ずしも正しいとは限らないため、「仮説の正しさ」を証明するために「検証」を行う必要があります。
■仮説形成の例②
・前提①:太郎を見つめる花子の目がハートになっている。【観察事実】
・前提②:人が異性を好きになると、目がハートになる。【一般法則】
・結論:だから、花子は太郎に恋しているぞっ! 【仮説】
※身近なものごとに目を向けて、このような例文を自分でも考えてみましょう。
■誤った仮説形成の例
①「太郎君が珍(めずら)しく学校を休んだ。」【観察事実】
②「宇宙人にさらわれると、学校に来ることができない。」【一般法則】
③「だから、太郎君は宇宙人にさらわれたに違いない!」【仮説】
※宇宙人の存在を既定(きてい)の事実とした「前提(②)」を都合よく持ち出して推論したために、「論理的に飛躍した(誤(あやま)った)仮説」が導出されました。このような例文を自分でも考えてみましょう。
・物理学者のニュートンは、「リンゴが木から落ちる」という「観察事実」をもとに、一般法則に照らすのみならず、その「創造的な想像力」によって思索(しさく)をめぐらし、ついに「引力」という未知の作用を「創案=仮説形成」しました。創案(そうあん)とは、今まで誰も考えつかなかったことを最初に考え出すことです。また、理論物理学者のアインシュタインも、「科学的仮説や理論というものは、観察された事実を説明するために『発明されるもの』である」と述べ、一般法則に縛(しば)られず、「創造的な想像力」を発揮して合理的な「仮説」を創案することの重要性を指摘しています。仮説形成は、科学においてだけでなく、日常生活においてもまた、さまざまな物事に対処したり、新しい考えを創案したりするうえで重要な役割を果たす強力な思考法の一つなのです。
※思索(しさく):物事の道理をたどり、秩序立てて深く考えを進めること。
⑤ アンカリング効果(初期値提示誘導)
■例えば、「ピザ」という語を相手に10回繰(く)り返させた後、「肘(ひじ)」を指差して「これは何か」と問うと、相手がつい「ヒザ」と答えてしまう現象を経験することがある。あるいは、ある商品の値札に書かれてある「元の値段」が二重線で消され、併(あわ)せて「割引価格」や「値下げ価格」が書かれてあると、それを見て「この商品は得だ」という印象を抱(いだ)いてしまうこともある。
・このように、「最初に提示された情報」が「アンカー=基準(初期値)」となって、その後の判断に影響が及ぶ心理現象を「アンカリング効果」という。論理的には「前提操作」の一種。
※アンカー:船の錨(いかり)のこと。最初に与えられた情報が「アンカー」となって心にとどまり、その後の思考や判断がその「アンカー」に引っ張られてしまう心理現象を「アンカリング効果」という。
■剽窃について
■当サイトのコンテンツを剽窃しているサイトが複数存在します。
①当サイトの記事、「枕詞一覧表」を剽窃しているサイト。
・「枕詞30種の表」が本サイト改編前の内容と完全に同一です。ネット記事をコピー&ペーストしただけで作成されている同業者によるサイトのようです。
②当サイトの「時間配分」の記事を剽窃しているサイト。
・多少文面が加工されていますが、内容は完全に同一です。
③当サイトの「俳句・短歌の通釈」を剽窃しているサイト。
・画像も当方が素材サイトから一枚一枚収集したものをそのまま掲載しています。
④他にも本サイトの記事をコピー&ペーストしただけで作成されているブログやサイトが複数あるようです。

